029 Trincubinquadism
2009-07-28 Filed in: Trincubinquadric
This glyph system shows one example of how we can modify Trincubinquadric glyphs, (base 432), to create corresponding glyph systems for three other bases.

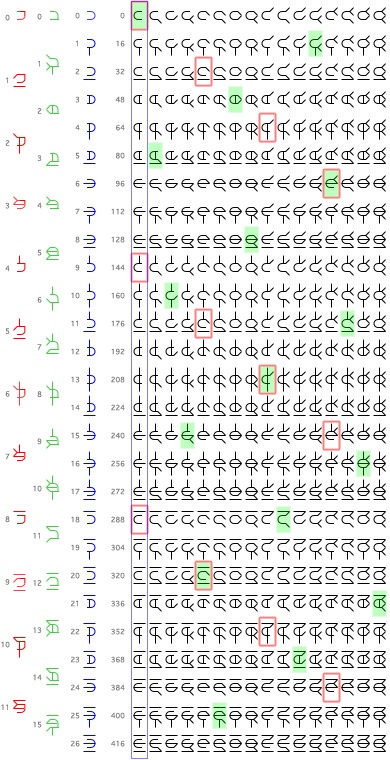
To the right of that, we see where the glyphs came from, a chart showing the glyphs used for base 432.
432 is the least common denominator of 12, 16, and 27, and may prove to be a useful base system for converting between bases 12, 16, and 27.
432 / 12 = 36. If we start at zero in base 432, we can jump in steps of 36 to acquire the 12 glyphs that can be used to represent base 12. (see the first column in red).
The glyphs are flipped horizontally and the arch that holds the glyph together is pinched to form a corner in the upper right. This is done to differentiate it from Tricubinqurdric.
432 / 16 = 27. If we start at zero in base 432, we can jump in steps of 27 to acquire the 16 glyphs that can be used to represent base 16. (see the second column in green).
Again, the glyphs are flipped, but in this system we will pinch the arch at the lower right side.
432 / 27 = 16. If we start at zero in base 432, we can jump in steps of 16 to acquire the 27 glyphs that can be used to represent base 27. (see the third column in blue). The glyph is flipped. No alterations are made to the arch.
The beauty of this system is that any number in these three bases can be flipped into base 432. This could lead to easier conversion and interaction between all four systems.
One downfall of this system is it’s complexity. The number one in base 16 uses six lines to represent itself. This seems ridiculous to me, but it leaves me thinking, are there simpler designs that can incorporate the same mechanics?

