019 Binquadratetric (65536) Introduction
2008-06-07 Filed in: Binquadratetric | Introductory
Base 65,536? Am I crazy? Maybe. This base glyph system toggles on and off 16 segments to create 65,636 different combinations. It is really just a compact form of displaying 16 binary digits.
Unfortunately, it does not contain many factors, especially when you consider it’s size: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, 16384, 32768, 65536.
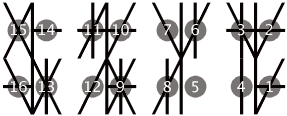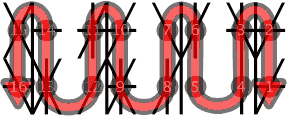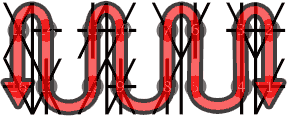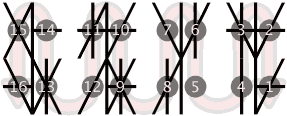
Each glyph contains four quadrants. It’s easier to differentiate the glyphs by breaking them down into their individual quadrants. Each quadrant can be thought of as a sub-digit of binquadric (hexadecimal).
Each sub-digit of binquadric toggles on and off four segments to create sixteen different combinations. The chart above shows the numerical value of each Binquadric sub-digit. Similar to Binquadric numerals, a specific segment is used to represent each binary sub-digit:
1 = Vertical Line
2 = Back Slash
4 = Horizontal Line
8 = Slash
These Binquadric sub-digits start at the lower right quadrant and wrap up and around to the other side. The pattern is continued to the next glyph. This creates a snake like sinusoidal pattern of reading which cuts down on unnecessary eye movement.
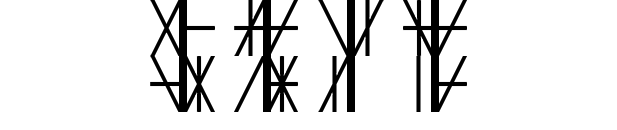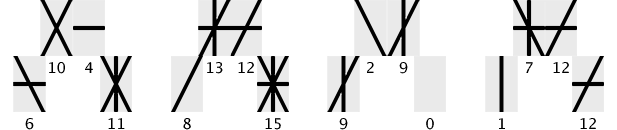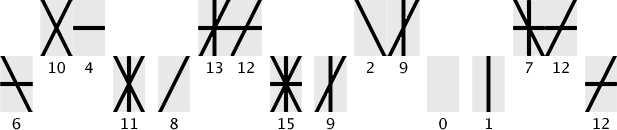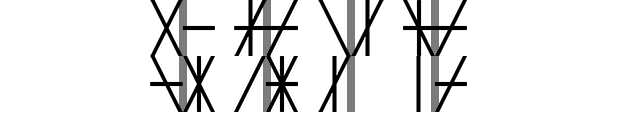
This example above shows a four digit Binquadratetric number and its sixteen sub-digits of Binquadric. If we rearrange the quadrants into a strait line, we can see the string of Binquadric sub-digits a little better.
.... UNDER CONSTRUCTION, MORE TO COME...
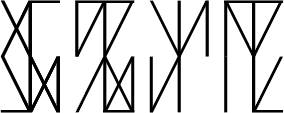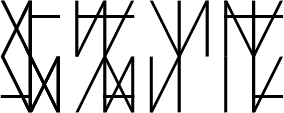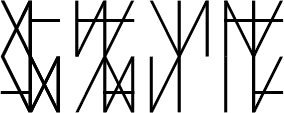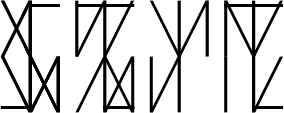
Alternative
Here are some animated examples of three digit numbers in Binquadratetric. A three digit binquadratetric number can range anywhere from zero to 281,474,976,710,656. (281,474,976,710,656 equals two to the power of forty eight)
