015 Trincubic Pronunciations
2006-05-11 Filed in: Trincubic
Seems silly, doesn’t it, making up totally different names for numerals?

The letter C is the third letter in the alphabet. Words and numbers use different writing systems, yet both have a numerical sorting sequence. What if they used the same system of symbols? Instead of using letters, just use the numbers. If the letter C is the 3rd letter in the alphabet, just write it as 3. Things could get unnecessarily complicated. One would need to determine if a sequence refers to numbers or words.
This simple concept of separation can be applied to the naming convention of our base systems. We differentiate systems to avoid confusion, so why not explore the idea of representing different base systems with different numerals AND different names.
If we assign consonants and vowels to different ternary sub-digits that appear in different positions of the glyph, we can create a naming system that corresponds to the mathematical structure of a Trincubic number.
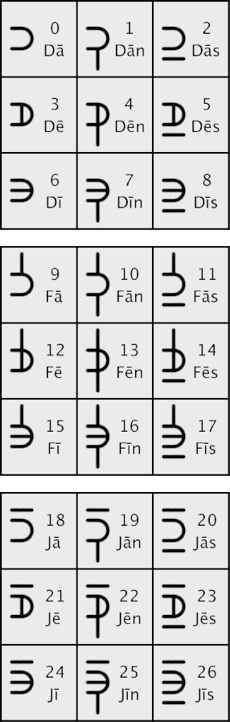
All number names could start with one of three different consonants; D, F, or J. These letters seemed like a good choice because they have dramatically different sounds to help differentiate the pronunciations:
D as in “Day”
F as in “Fake”
J as in “Jade”
One of three vowels are used in the middle of the name to differentiate it further. The vowels use the long version of pronunciation, indicated with a Macron.
Ā as in “ate”
Ē as in “eat”
Ī as in “pie”
The ending sound for each number uses N, S, (or none). These letters were chosen for their unique ability to blend sounds together.
N as in “Jane”
S as in Chase”
For example, the base twenty seven number, 9468, can be pronounced: Fadendidis,
(phonetic: Fay-Dean-Die-Dice). One syllable is used for each number. Syllables can easily blend together into easily pronounced, short, discernible words.
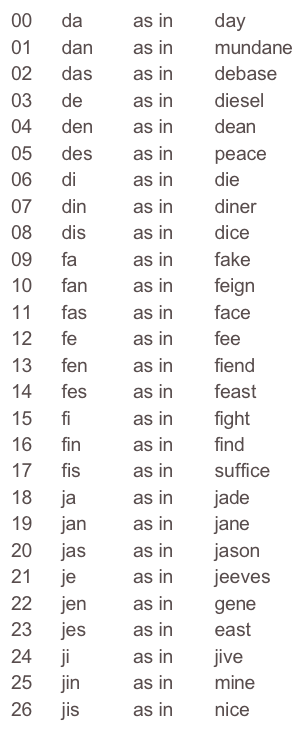
I have assigned all the letters in alphabetical order, so the names of the numerals sort corresponding to their quantities.
D before F before J
A before E before I
_ before N before S
Well, as I said, a strange idea. Ends up sounding a little bit like german, or like it was lifted out of a Star Trek episode.
Keep in mind that anything new will seem alien at first, but imagine what things would be like if this was the norm. How long does it take a child to learn about numbers and their names. At least this system offers a pattern of logic to it.
Of course, this system is biased to the English language, but there is a larger concept here that is more important. Is there a way to design relationships between number systems and language systems that can benefit the users of those systems?

