012 Introduction to Trincubic Glyph Rotation

These rotations can also be performed in a three dimensional space, even though the numerals are written on a two dimensional surface.
Let’s use the number five as an example. In Trincubic, it is written as a backwards C with a vertical segment in its center and a horizontal segment below. The area above the backwards C is blank. The blank space actually represents a segment that runs in the direction of front to back. Whenever a blank area appears, imagine it as a segment that starts at your eye and runs away from you.
The formal written form of Trincubic uses dots instead of blank spaces to better represent this direction on a two dimensional writing surface. In this site, the simplified, casual form is used instead. It seems overkill to always use dots when a blank space gets the message across just fine. But in the case of Rotations, it can help us, because a line running front to back, looks like a dot. So if it helps, fill in your blanks with dots.
0 — Blank Space — Line Running Front Back
1 — Vertical Line — Line Running Up Down
2 — Horizontal Line — Line Running Left Right
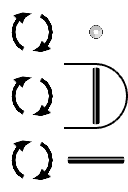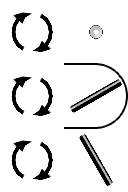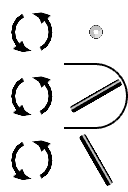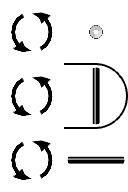
CW/CCW Rotation ( Bank ) { Roll } [ Z ]
A ternary zero is represented as a segment that runs front to back. If we rotate it clockwise or counter clockwise, it will spin like a log in a river. It will not change its axis. The segment direction remains unchanged. The other segment directions will change though. A vertical segment rotates into a horizontal segment, and vice versa. The number five is transformed into a seven.
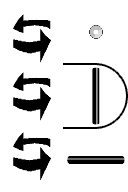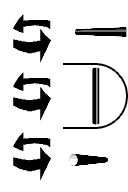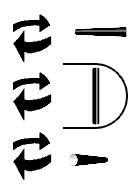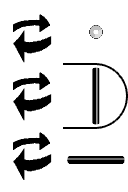
Frisbee Rotation ( Heading ) { Yaw } [ Y ]
A ternary one is represented as a vertical segment. If we spin the segment like a top on a table or a frisbee flying through the air, it will not change its axis. The segment direction remains unchanged. The other segment directions will change though. A horizontal segment will spin to appear edge on, looking like a dot. A segment seen edge on, appearing as a dot, spins and turns into a horizontal segment. The number five is transformed into the number twenty-one.
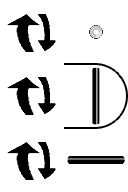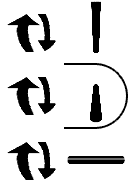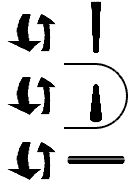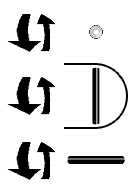
Tire Rotation ( Pitch ) { Pitch } [ X ]
A ternary two is represented as a horizontal segment. If we rotate it in a tire like direction, (as if you were observing the tire of a bicycle you were riding), the axis of the tire will not change (provided you always travel in a strait line). The segment direction remains unchanged. The other segment directions will change though. A front to back segment rotates into a vertical segment, and vice versa. The number five is transformed into an eleven.
Combinations
A trincubic number can be rotated several times to produce different combinations of numbers. However, there are only six different combinations that can be achieved.

