008 Three Sub-Digits of Ternary
2006-04-23 Filed in: Trincubic
Each trincubic numeral is really just a way to group three ternary numbers together in a compact form.


A vertical line is used to represent 1 and a horizontal line is used to represent 2. (zero is represented as a blank area.)
A flipped C symbol is used to outline the three different positions that the ternary sub-digits can appear; below, middle and above.
This gives us 27 different combinations, 3x3x3, (3^3). It seems strange to have a number system that has an odd amount of numerals in it, but it does have some advantages worth exploring.
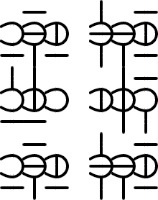
Centipede Formation
The numerals can then be connected together to make them even more compact. Glyph connection can signify the boundaries of a complete number, or it could be used for visual separation, similar to how decimal numbers are broken up with commas every three digits.
Legacy Comments:
Ron
Thursday, August 13, 2009 - 03:53 PM
Here is something interesting - the digits of base 27 can be graphically represented on a cube. Place 1 and 2 on two opposite faces of the cube. Then place 3 and 6 on another pair of opposite faces, and 9 and 18 on the remaining faces. Each edge is the graphical and mathematical union of the two faces that meet there, and each corner is the graphical and mathematical union of the three faces that meet there. (In other words, if the three digits that meet at each corner are drawn on mylar and stacked together, they make a new digit - so 17 is just 9, 6, and 2 stacked together). This procedure uses all the digits once - except zero, which can be placed in the center of the cube. Numbers on opposite faces, corners, and edges add to some number that is zero mod 3 (which graphically speaking means that if they're stacked together, you'll have either a space or a cross in each sub-digit-place). The same procedure works in base 81, 243, 729 etc., with the cube of the appropriate number of dimensions (4D hypercube, 5D hypercube, 6D hypercube, etc).

