006 Four Sub Digits of Binary
2006-04-23 Filed in: Binquadric
Binary numbers are the building blocks behind computers. This system uses four slanted segments to represent binary digits.

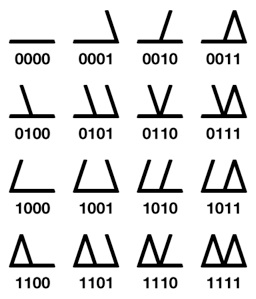
A horizontal line is added to hold the glyph together as the segments toggle on and off. This creates sixteen different combinations.
The segments toggle on and off in a binary pattern. The upper right illustration shows the similarities. Converting Binquadric into binary becomes easy. Even large numbers using several numerals will instantly morph into binary, just by removing the horizontal rules and straitening out the slants.
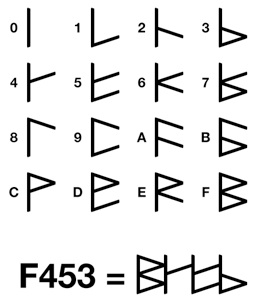
Though it’s useful having a binary pattern clearly visible running left to right, I have found that rotating the numerals also has benefits.
The glyphs take up less space horizontally, allowing large numbers to occupy less room.
You can even connect numerals together to signify digits of a large number. Why have spaces if we don’t need them?
The vertical line creates a frame around the slanted segments, making it easy for the eye to pick out each digit, (although, you will see gaps if a zero appears in the number, so it’s questionable if this is a good idea).
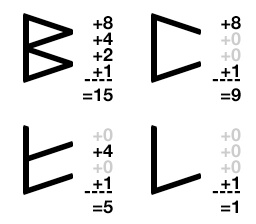
We spend a lot of time as children learning numbers, their amounts, their names. This system offers easy patterns that you can teach a child. Schemas can be built at an earlier age.
The mind starts to think of numbers as groups of powers of two, (15=8+4+2+1), (9=8+1). I believe that there are benefits to thinking this way.

